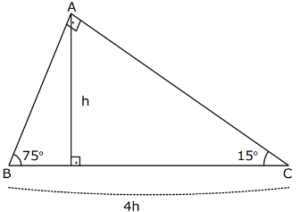
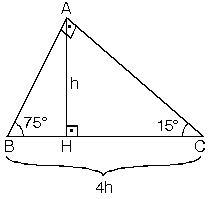
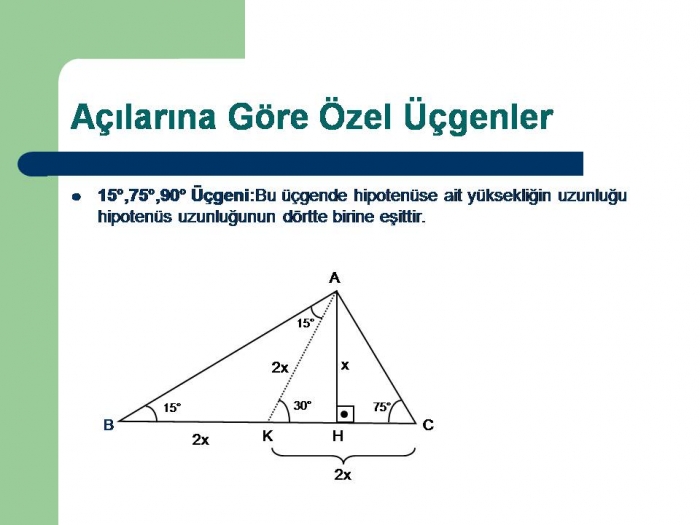
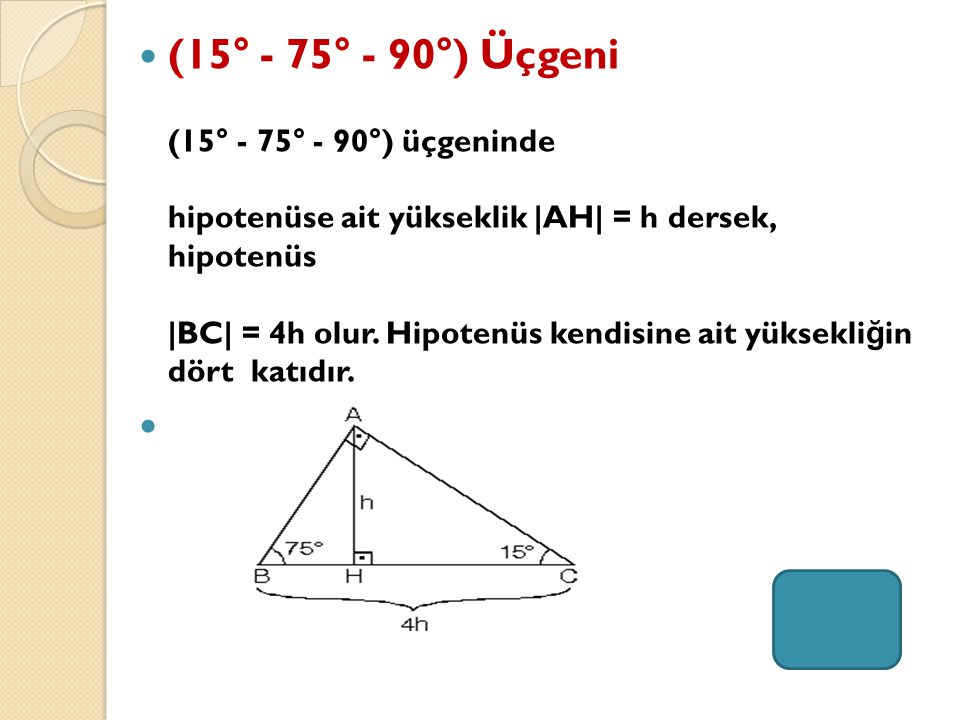
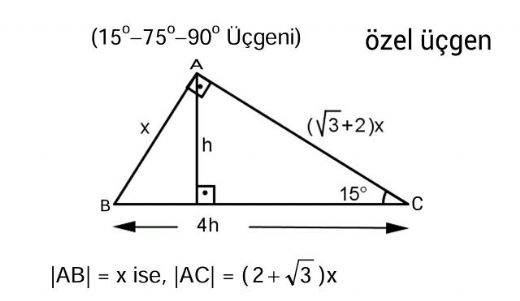
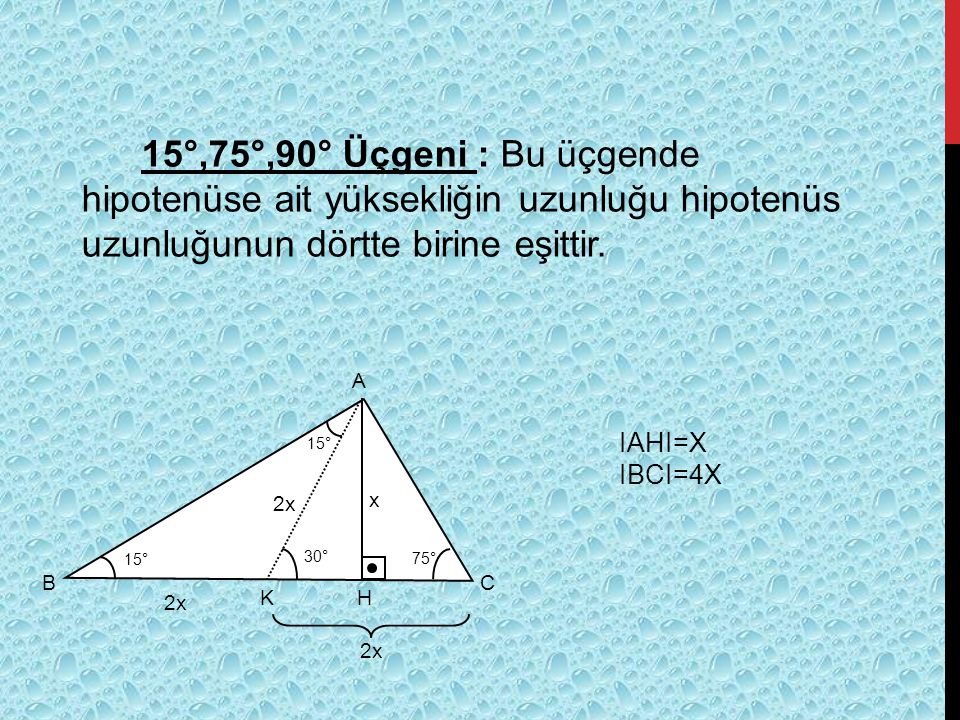
L content, and share 6 with friends, family, on world on resim L content, and share 6 with friends, family, on world on 最も共有された! √ 90 75 15 Ucgeni Ozelligi 中学 地理 resim ;7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = ラベル 75 15 90 üçgeni özellikleri の投稿を表示しています。すべての投稿を表示(15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, Hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır İKİZKENAR ÜÇGEN İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem

Dik Ucgen Wikiwand
15 75 90 üçgeni kenar özellikleri
15 75 90 üçgeni kenar özellikleri-75 15 90 üçgeni özellikleriÖzel Üçgeni ve Özellikleri 8Sınıf Matematik 22,567,590 Üçgeni ve Özellikleri (Bağıntıları) 8Sınıf Matematik Son Eklenen İçerikler15 75 90 üçgeni ile ilgili bilmemiz gereken ve çok basit olan bir dikme özelliği vardır 15 75 90 üçgeni içerisinde 90 dereceden hipotenüse indirilen bir dikmenin uzunluğu hipotenüsün 4'te biri kadar olur Etiketle r 15 75 90 üçgeni özelliklerinin ispatı, 15 75 90 üçgeni özellikleri nelerdir, 15 75 90 üçgeni özellikleri nerden geliyor, hipotenüs neden yüksekliğin dört kat ı s # Bora Arslantürk # ispat # matematik # son # video Tweet Share Pin it zaman Bunu Epostayla Gönder BlogThis!




Dik Ucgen Ozellikleri Nelerdir Egitim Haberleri
özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeni Geometrideki özel üçgenlerden biri de 15 75 90 üçgeni dediğimiz özel üçgendir Bu üçgen karşımıza diğer özel üçgenler kadar yaygın çıkmasa da üçgenini bilmek bize geometride birçok yerde fayda sağlayacaktır Çünkü bu üçgen türü karşımıza tek başına çıkmasa dahi soru içerisinde çıkabilmektedir 15 75 90 üçgeni ile ilgili özellikleriABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipotenüse ait yükseklik;
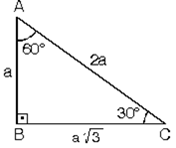
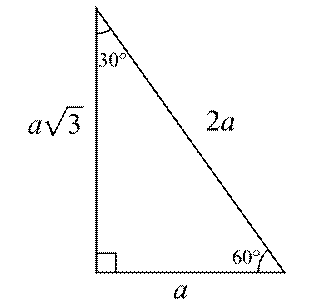
5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC =15 75 90 üçgeni özelliklerinin ispatıDaha fazla ispat için http//wwwozelderscicom/matematikformullerininteoremlerininhtmlSitemizi ziyaret e15 75 90 Üçgeni Özellikleri ve Kuralları Geometri dersi için özel üçgenlerin büyük önemi bulunmaktadır Özellikle bu tür üçgenlerin özellikleri bilindiğinde pek çok soru çok rahat bir şekilde çözülmektedir 15 75 90 üçgeni de bu özel üçgenler arasında özellikle bilinmesi gereken üçgenler arasında yer almaktadır
HD限定75 15 90 üçgeni özellikleri Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir 15 75 90 Ucgeni Webders Net 15 75 90 Ucgeni Not Bu 15 75 90 Ucgeni Uludag Sozluk4 (30° – 60° – 90°) Üçgeni 5 (30° 30° 1°) Üçgeni 6 (15° 75° 90°) Üçgeni ÖKLİT BAĞINTILARI Sponsorlu Bağlantılar Dik açılı üçgen, iç açılarından biri 90° olan üçgendir Çemberde çapı gören çevre açı 90°'dir Bir dik üçgende kenarlar arasında a2 = b2 c2 bağıntısı vardır90 15 75 ucgeninin ozelligi vardır 15 75 90 üçgeninde dikme özelliği Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz 30 60 90 üçgeni 15 75 90 üçgeni özelliği bu makaledeki notlar En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmas şekilde m 90 kenarı hipotenüs ve Mutlu olmak için gerekenler 11;




15 75 90 Ucgeni Akilli Geometri



1
これまでで最高の75 15 90 Miter Angles And Miter Saws Thisiscarpentry Angle Sums And The 15 75 90 Right Triangle Geogebra Finding The Area Of A 15 75 90 Triangle With The Length Of The15 75 90 Üçgeni Özellikleri acilargentr Üçgeni (2√3) İSPAT Dik Açılı Üçgen, Kenarlarına Göre Üçgenler acilargentr Dik Açılı Üçgenin Kenar ve Açı Özellikleri Nedir üçgeni 22,5 67,5 90 Üçgeni (1√2) İSPAT Dik Üçgen Konu Anlatımı ve Örnek Soru Çözümü Kunduz Popüler İçerik ucgengentr Dik üçgen Geometri dersinin önemli konuları arasında yer alan özel üçgenlerin bilinmesi soru çözümleri ve sınava hazırlanan öğrenciler için büyük bir avantajdır Bu özel üçgenlerden olan 45 45 90 üçgeni ise bir ikizkenar dik üçgendir ve sorularda sıkça öğrencilerin karşısına çıkmaktadır Bu üçgen bir ikizkenar üçgen olduğundan ikizkenar üçgen kurallarının




Murat Sen Akdeniz Universitesi Ucgenler Ppt Video Online Indir



Q Tbn And9gcto4bnkzt2y Mlslzezgmlwske7ayni5axjtwi4doy0xjos1y Usqp Cau
Özel üçgenlerden bilinmesi gereken üçgenlerden bir tanesi de 15 75 90 üçgenidir Bu üçgenin bilinmesi soruların çözülmesi açısından basitlık sağlamaktadır 15 75 90 üçgeni bir dik üçgendir Her üçgende olduğu gibi iç açıları toplamı 180, dış açıları toplamı ise 360 derecedir Bu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 7575 lik üçgeni 60 ve 15 e ayırarak 30 60 90 üçgeni oluşturmadan çözemediğim özel üçgen 1 1312 crocodile # entry adresi şikayet et Aynı şekilde 45 45 90 üçgeni, 15 75 90 üçgeni ve 30 30 1 üçgeni de önemli özel üçgenler arasındadır Bu yazıda biz 30 60 90 üçgenine odaklanacağız 30 60 90 Üçgeni Trigonometrik Oranları 30 60 90 üçgeninde 30 derecenin15 75 90 ÜÇGENİ VE ÖZELLİKLERİ ÖKLİT BAĞINTILARI HAKKIMIZDA Bu sayfada yer alan bilgilerin her hakkı, aksi ayrıca belirtilmediği sürece TestDefteriCom'a aittir Sitemizde yer alan dosya ve içeriklerin telif hakları dosya ve içerik gönderenlerin kendilerine veya yetki verdikleri kişilere aittir Sitemiz hiç bir şekilde kâr amacı gütmemektedir ve sitemizde yer alan




15 75 90 Ucgeni




Ozel Ucgenler Not Bu
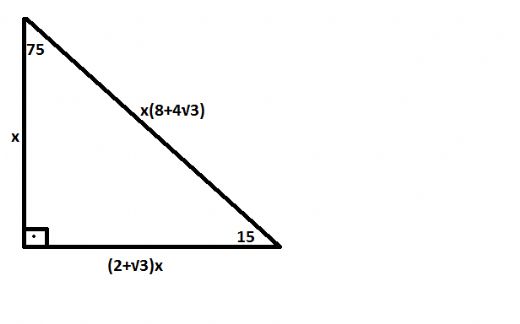
A) 2 3 4 B) 2 3 6 C) 4 3 2 D) 4 3 4 E) 4 3 6 wwwmatematikkolaynet Çözüm 15 75 90 üçgeninden AD 8 4 3 olur ABD ve HAD üçgenleri benzer üçgenlerdir Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeni Enes Ergel bu konuyu 9 sınıf matematik soruları forumunda açtı Cevap 2 Son mesaj 12Angle Sums and the Right Triangle – GeoGebra Math off the grid Alternate Forms 90 75 15 Üçgeni, 90 75 15 Üçgeni Özellikleri ucgengentr Finding the area of a $$ triangle with the length of 問國中數學 閒聊板 Dcard Variables on Both Sides 0CHS Algebra Website 1314 Gebhard, Curt / PreCalc Notes Deriving Sines and Cosines Tonic
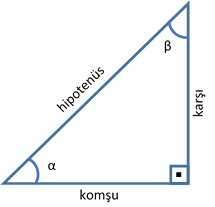



Dik Ucgende Trigonometrik Hesaplamalar



Ucgenler Alkan Hoca Matematik Yks Tyt Ays Kpss Ales Dgs Ygs Lys Teog
15 75 90 üçgeni özellikleri Bir dik üçgendir İki dar açısının toplamı dik açısını vermektedir İki dar açı karşısındaki dar kenarlarının toplamı her daim dik açının karşısındaki geniş kenar uzunluğunu vermek zorundadır İki dar açının oranı 1/5 olmak zorundadırÜçgeni (2√3) İSPAT Dik üçgen 15 75 90 üçgeni işlemli em iyi secicem gereksiz Dik Üçgende Trigonometri Bikifi Finding the area of a $$ triangle with the length of Finding the area of a $$ triangle with the length of Mark Wadsworth The right angle triangle Math off the grid And yet more fun Exact Trig Values Diküçgeni kenarları arasındaki oran ekşi up Üçgeni (2√3) İSPAT 15 75 90 Üçgeni Not Bu triangle Math, Trigonometry, Right Triangles ShowMe Finding the area of a $$ triangle with the length of What are the side relationships of a triangle?



Ozel Dik Ucgenler Delinetciler Portal




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List
子供向けぬりえ ベスト5075 15 90 üçgeni özellikleri 15 75 90 ucgeni 90 45 45 üçgeni Dik üçgen Vikipedi 22,5 67,5 90 Üçgeni (1√2) İSPAT 最も共有された! √ 90 75 15 Ucgeni Ozelligi 中学 地理 Pisagor Teoremi İspatı Geometrik Yöntem Dik üçgenler, Pisagor Teoremi konu anlatımı soru çözümleri 15 75 90 üçgeni uludağ 15 75 90 üçgeninde 90°'lik açının karşısındaki kenarın (hipotenüsün) uzunluğu (√2 √6)k 'dir 15 75 90 Üçgeni Özellikleri 1 15 75 90 Üçgeninin kenar uzunluklarının toplamı (√2 √3 √6 √9)k 'dir(15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, Hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır İKİZKENAR ÜÇGEN İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır 1 Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen




Geometrik Kavramlar Geometride Nokta Dogru Duzlem Gibi Kavramlar Tanimsiz Olarak Kabul Edilir Ppt Indir




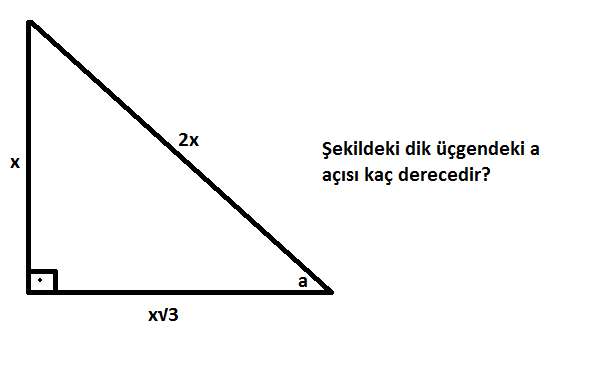
3 4 5 Ucgeni Ve Ozellikleri Not Bu
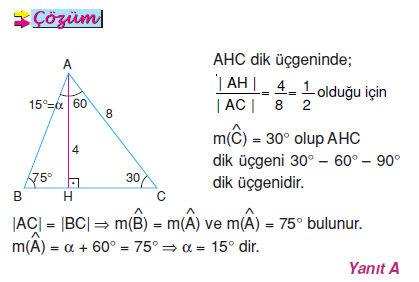
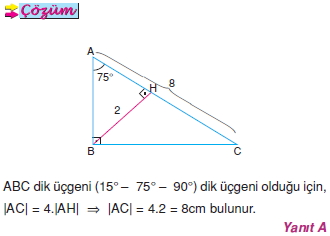
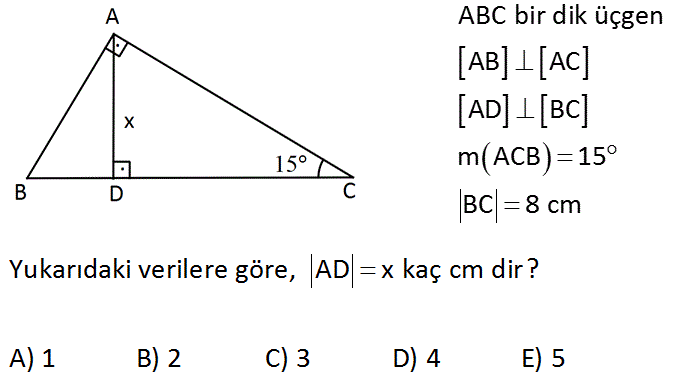
AD C üçgeni 15 75 90 üçgenidir 15 75 90 üçgeninde hipotenüse inen yükseklik, hipotenüsün 4' te 1'i dir 4 2 x 2 cm bulunur 4 12 ABC eşkenar üçgen, AB // AD AE AD ED 2 cm Yukarıdaki verilere göre, BE x kaç cm dir? üçgeni aynı zamanda kenarlarını da etkilemektedir Böylece açıların karşısındaki kenar ile beraber diğer kenarları üzerinden belli bir bağıntı bulunur Bu bağlantı sayesinde hem kenarlar hem de açılar kolay bir şekilde bulunabilmektedir 30 60 90 Üçgeni Nedir?üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu




Pdf Influence Of Foreign Ions On The Crystal Structure Of Batio3




Geochemistry Of The Middle Jurassic Sediments In Gumushane North Eastern Turkey Implications For Weathering And Provenance Saydam Eker Geological Journal Wiley Online Library
Teoremin kendine has özelliklerinin olmasıdır Bu özellikler başka hiç bir teoremde yada cisimde bulunmamasıdır En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmasıdır Üçgenlerin 3 adet kenarı ve 3 adet açısı vardır90 75 15 Üçgeni, 90 75 15 Üçgeni Özellikleri ucgengentr PythonMatplotlib boxplot How to show percentiles 0,10,25 triangle Math, Trigonometry, Right Triangles ShowMe 15 75 90 Üçgeni Üçgende Açılar Ders Notları Kunduz Math off the grid Alternate Forms gnuplot demo script spiderplotdem Üçgeni (2√3) İSPAT 問國中數學 15° 75° 90° üçgeni, Özel bir üçgendir Matematikte özel kavramı;




22 5 67 5 90 Ucgeni Ozelligi Matematik Sarisin Renkli Okuma




Dik Ucgen Wikiwand
15 75 90 Üçgeni Özellikleri Sorularda bir üçgene, bir dikdörtgene ya da herhangi bir çokgene dikme indirerek veya bir çizgi çekerek karşınıza 15 75 90 üçgeninin çıkmasını sağlayabilirsiniz Bu üçgeni bulduktan sonra aşağıdaki kuralları aklınızdan çıkarmamanız gerekir Dik üçgendir Bu üçgenin iki dar açısını topladığınızda dik açısını bulursunuz75 15 90 ucgeni kenarlari üçgeni kenarları arasındaki oran ekşi up Üçgeni (2√3) İSPAT triangle Math, Trigonometry, Right Triangles ShowMe 15 75 90 Üçgeni Üçgende Açılar Ders Notları Kunduz Finding the area of a $$ triangle with the length of 15 75 90 üçgeninde 15 derecelik açının karşısında ki kenar 1cm olarakIkizkenar 15 75 90 Ucgeni Yardim Edebilir Misiniz Cozemedigim 75 15 90 özel üçgeni bu özel üçgende 15 derecelik açının karşısında yer alan kenar uzunluğu 1cm alınırsa 75 derecelik açının karşısındaki kenarın uzunluğu 2 3 cm olur şekildeki gibi iki üçgene ayırırsak 15 15 150 ve 30 60 90 labla ise lbdla3 olacaktır ve




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com




30 60 90 Ucgeni Ve Ozellikleri Not Bu
15 75 90 Üçgeni Özellikleri ve Kuralı Öğrenci Yardım Exact Trig Values Math off the grid Alternate Forms Popüler İçerik ucgengentr Math off the grid Some interesting relations fall out DİK VE ÖZEL ÜÇGENLER TEST2 » Ders Geometri Mark Wadsworth The right angle triangle The Triangle RobertLovesPinet Üçgeni (2√312 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1 x x x 3 Bu üçgende, 1 nin karşısındaki kenar, eş kenarlardan birinin 3 katına eşittir AB = AC mEitim 15 75 90 Üçgeni Özellikleri ve Kuralı Öğrenci Yardım resim;




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com



1
Twitter'da Paylaş Facebook'ta Paylaş 'te Paylaş s5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur90 75 15 Üçgeni, 90 75 15 Üçgeni Özellikleri ucgengentr img Math off the grid And yet more fun img Angle Sums and the Right Triangle – GeoGebra img #75 #90 Combo Embroidery Needles img 15 75 90 Triangle Side Lengths img triangle Math, Trigonometry, Right Triangles ShowMe



Dik Ucgen Konu Anlatimi Bilgicik Com Bilgicik Com




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger Hepsi Konu Anlatimi
Quora Angle Sums and the Right Triangle – GeoGebra Math off the gridエレガント90 75 15 üçgeni The 27 63 90 Triangle Robertlovespi Net Dik Ucgen 16 15 75 90 Ucgeni Evde Egitim Ders Calisma Ipuclari 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki Üçgenler geometride ve hayatın birçok alanında karşımıza çıkmaktadır Üçgenler konusu öğrencileri de çok ilgilendiren bir konudur Sınavlarda üçgenler
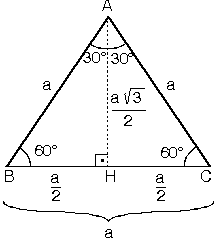



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Sinavlarda Hic Sorulmadi Sorarlar 22 5 67 5 90 Ucgeni Youtube
15 75 90 üçgen özelliği ve 15 75 90 üçgeninin 2 pratik kuralı ve örnek çözümlü sorularPratik Geometri Yöntemleri videolarımda sizlere mantık ve pratik yönteGold Edition only helps to enhance15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgend




Genler Gen Etler Ekenar Gen Kzkenar Gen Dk
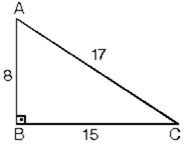



Dik Ve Ozel Ucgenler 1
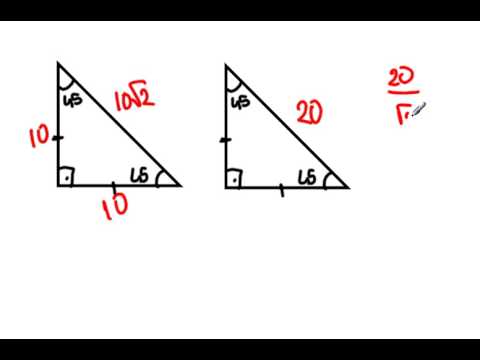
15 75 90 Üçgeni Özellikleri ve Kuralları Geometri dersi için özel üçgenlerin büyük önemi bulunmaktadır Özellikle bu tür üçgenlerin özellikleri bilindiğinde pek çok soru çok rahat bir şekilde çözülmektedir 15 75 90 üçgeni de bu özel üçgenler arasında özellikle bilinmesi gereken üçgenler arasında yer almaktadır 15 75 90 Üçgeni Özellikleri 15 75 90 Üçgeninde Kenarların Oranı 15 75 90 üçgeninde kenarlar arasında belirli bir oran bulunması zorunluluğu vardır Bu oran formül ezberlendiği zaman rahat bir şekilde ortaya çıkartılabilir Eğer formülü ezberlemezseniz farklı yöntemlerle bu hesaplamaları yapabilirsiniz Fakat oldukça yoğun bir zaman ayırmanız gerekiyor45 45 90 üçgeni özellikleri 45 45 90 üçgeni özellikleri Bölüm Geometri Durum Çözüld ü Tarih 1 yıl önce Adı Gün Işığı 0 kişi takip ediyor Takip Et Verilmiş Cevaplar gokturk En İyi Cevap 16 # Cevap 45 45 90 üçgeni ikizkenar dik üçgen 'dir İkiz kenar üçgenin özellikleri, İkizkenar üçgende ikizkenarlara ait yükseklikler




Acilar Ve Ucgenler




45 45 90 Ucgeni Youtube
Bu yazıda 15 75 90 üçgeni kenar bağıntıları ve özellikleri üzerinde kısaca durmaya çalışacağız Geometri dersinde özel üçgenleri iyi bildiğimiz zaman geri kalan üçgenleri de bu üçgenlere benzeterek soruları çözme yoluna gideriz Daha önce 30 60 90 üçgeni yazısında başka bir temel üçgenin özelliklerinden bahsettik Eğer kuralını bilmiyorsanız mutlaka 30 60 90 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğerNjoy the videos and you music upload original resim Njoy the videos and you music upload original Math off the




15 75 90 Ucgeni Pow Bylge




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
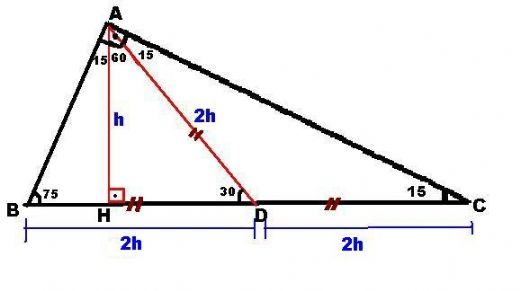
Üçgeni (h4h) İSPAT üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına h dediğimiz zaman 90⁰'nin karşısına 2h




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri



Ozellik 5 Bilgicik Com Bilgicik Com




Dik Ve Ozel Ucgenler



Ozel Ucgenler Konu Anlatimi




Dik Acili Ucgenlerin Ozellikleri Nelerdir Dik Ucgenlerin Temel Ozellikleri




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim




Blth0chdz3jm



Acilar Ve Ucgenler




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Ozellikleri Ve Sorulari



Dik Ucgen Vikipedi



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




45 45 90 Ucgeni



Acill Ozel Geometri Sorusu




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu




Nature And Genesis Of Potassic High Basr Granitoids Associated With Syn Convergent Extension In Nw Turkey Sciencedirect



Dik Ve Ozel Ucgenler 1




15 75 90 Ucgeni Ozelliklerinin Ispati Ozeldersci



15 75 90 Ucgeni Uludag Sozluk



1




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali



30 60 90 Ucgeni Kenar Oranlari Ispati Geometri Khan Academy Turkce




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube




The Geochemical Composition Of The Palu Formation From The Palu Uluova Basin Elazig Eastern Anatolia Turkey Implication Of Source Area Weathering And Tectonic Setting Sciencedirect




Dik Ucgen 17 22 5 67 5 90 Ucgeni Evde Egitim Matematik Ders Calisma Ipuclari




Ucgen Ve Ozellikleri Pisagor Arican Fen Bilimleri Facebook



Dik Ucgen Ozellikleri Nelerdir Egitim Haberleri




Modacar Tuvturk Uyumlu Ucgen Reflektor Metal Ayakli Fiyati




15 75 90 Ucgeni Webders Net




Dik Ucgen Formulleri



Ozel Ucgenler Ppt Video Online Indir




Late Jurassic Magmatism And Stratigraphy In The Eastern Sakarya Zone Turkey Evidence For The Slab Breakoff Of Paleotethyan Oceanic Lithosphere The Journal Of Geology Vol 125 No 1



Http Mufredat Meb Gov Tr Dosyalar Ttkb Lise 9 Matematik C2 Matematik 9 Pdf



ベスト 75 15 90 Ucgeni Ozellikleri シモネタ



Dik Ucgen Vikipedi




2 Kok 5 3 Ucgeni




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



90 75 15 Ucgeni Ozellikleri



15 75 90 Ucgeninin Ozellikleri Nelerdir




Nedir Dik Ucgen



Dik Ucgende Trigonometrik Oranlar




15 45 1 Ozel Ucgeni Var Mi Varsa Kurali Nedir Eodev Com




Jurassic To Cenozoic Magmatic And Geodynamic Evolution Of The Eastern Pontides And Caucasus Belts And Their Relationship With The Eastern Black Sea Basin Opening Hassig Tectonics Wiley Online Library



画像をダウンロード 75 15 90 Ucgeni Ozellikleri 子供のためのちょうど着色ページ




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir




Ozel Ucgenler Konu Anlatimi Ogretmen Tercihim



最新 75 15 90 Ucgeni シモネタ




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube




Ucgenler Icin 76 Fikir Evde Egitim Matematik Geometri




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com
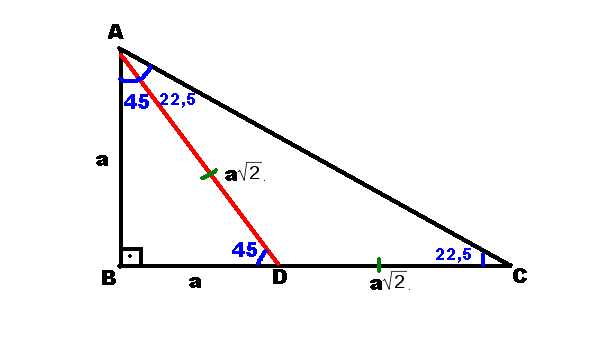



22 5 67 5 90 Ucgeni 1 2 Ispat
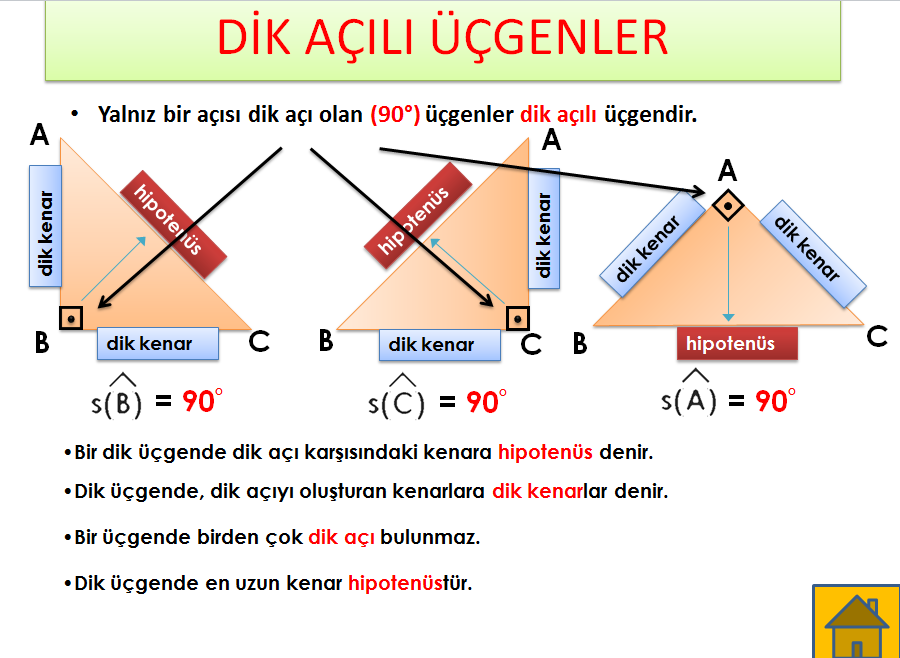



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Kenarlar



Dergipark Org Tr En Download Article File 0350




Zoqr8sxmfxasqm



15 75 90 Ucgeni
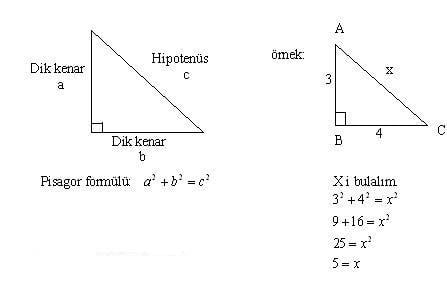



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



Http Mufredat Meb Gov Tr Dosyalar Ttkb Lise 9 Matematik C2 Matematik 9 Pdf
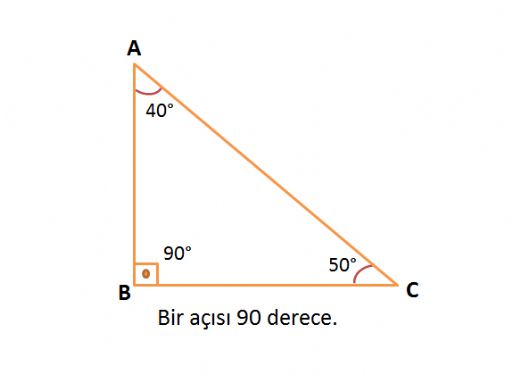



Dik Acili Ucgen Kenarlarina Gore Ucgenler




Dik Ucgen Ozellikleri Nelerdir Egitim Haberleri
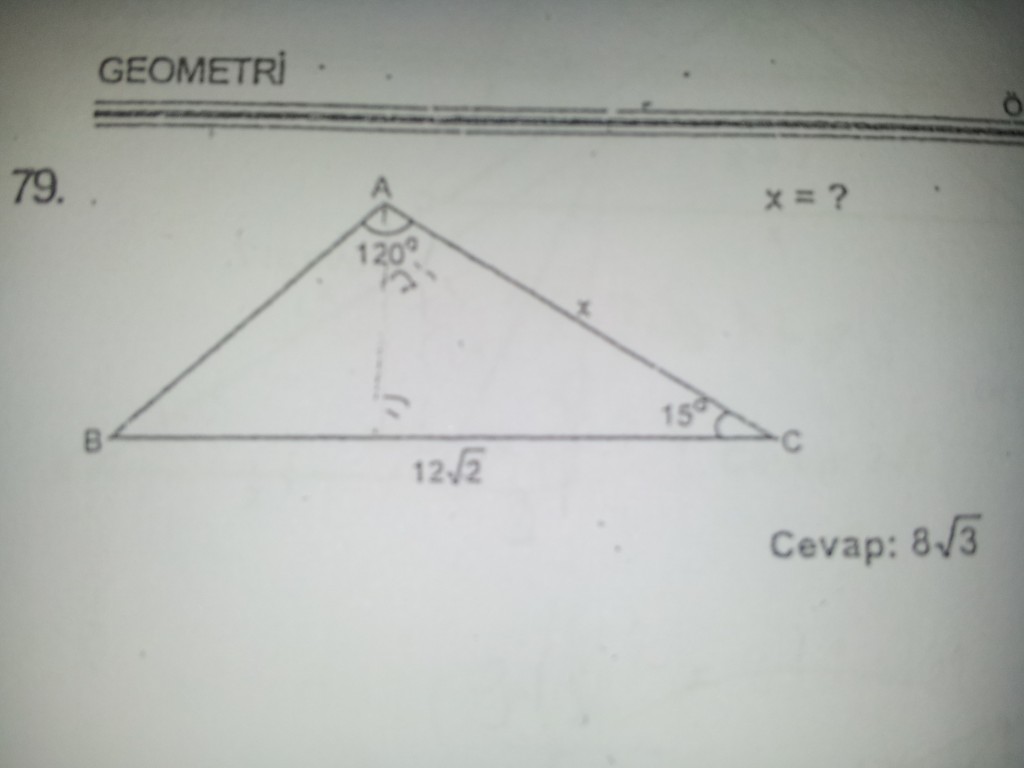



15 75 90 Ucgeni




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali



Http Www Balgatcozum Com Editor Img Userdir Marketing 04 Ygs Lys Hazirlik Dik Ucgen Pdf
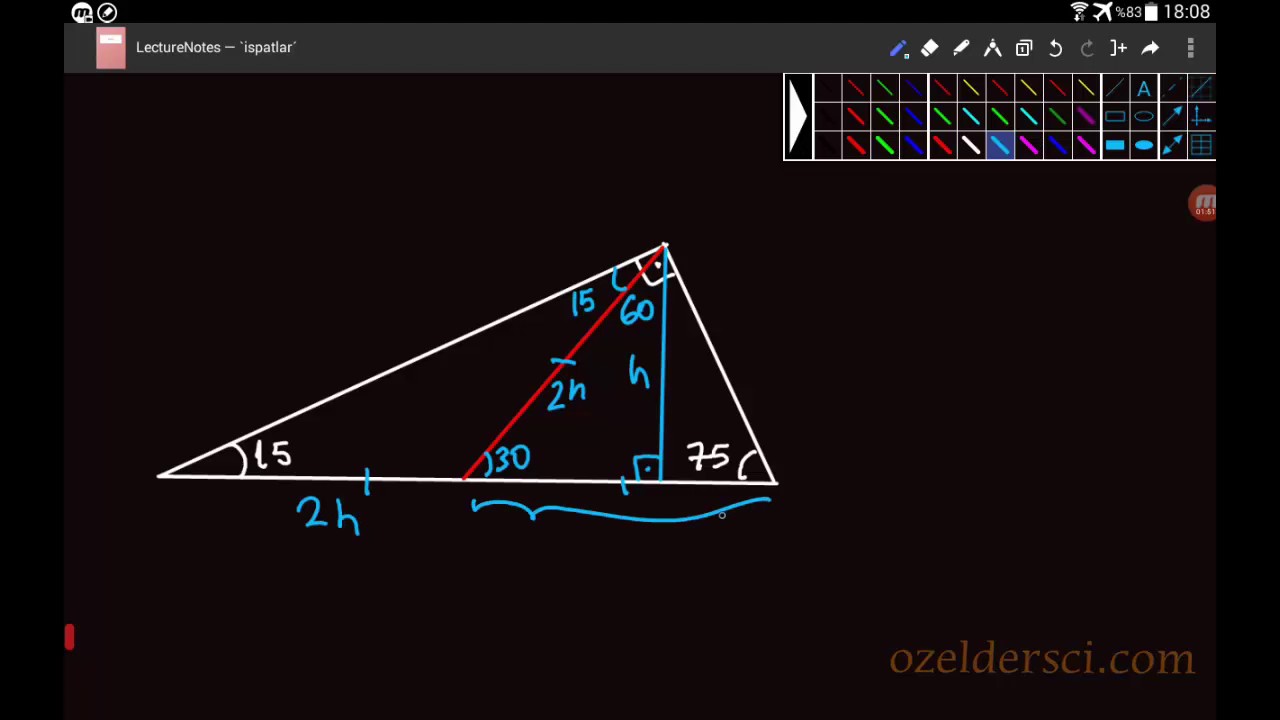



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube



45 45 90 Ucgeni Matematikce




Ucgende Acilar Cozumlu Sorulari Ve Problemleri Matematik Ogretmenleri



15 75 90 Ucgeni Ozellikleri




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube


